We live in a world of oscillations!! You can try keeping your body absolutely still but your heart will still beat and your lungs will still expand and relax. All the while, electrons move back and forth about 60 times/sec as part of the process to supply energy to the LCD screeen on your iPhone!

Oscillations are characterized as movement of an object back and forth around a specific point of equilibrium, that is, a point of zero force. Oscillations have a cycle, occurring as a repeating pattern. The time for one complete cycle is called the Period (T) of an oscillation.

The cyclic appearance of Venus proved Copernicus’ sun centric solar system!

The simplest form of oscillation occurs when the restoring force obey’s Hooke’s Law. That is, when the restoring force is directly proportional to the distance that the oscillating object is displaced from equilibrium. This is called an Ideal Spring.

F = -kx

The negative sign indicates that the force is always opposite the displacement.

Shelly exerts a force of 10 N on a spring, stretching it a distance of 20 cm.

(a) How far will the spring stretch if a force of 20 N is exerted on it?

(b) What is the spring constant of the spring?

Please enjoy the amazing Trey Anastasio manipulating SHM.

We know the Period (T) is the time it takes to complete one cycle in SHM. Frequency (f) is equal to the number of oscillations per unit time. We usually assign the unit Hertz (Hz) to frequency that basically means “anything per second”.

Since (T) is the number of seconds elapsed per cycle and (f) is the total number of cycles per second, it stands to reason that these quantities are reciprocals. This is very useful!

f = 1/T and T = 1/f

Farrah has a resting heart rate of 50 beats/min. When Farrah sprints a lap on the track, her pulse increases to 150 bpm. Compared to when she is at rest, the period of her heart rate when she is sprinting is

(a) 9x (b) 3x (c) same (d) 1/3x (e) 1/9x

(a) What is the oscillation period of your eardrum when you are listening to the A4 note on the piano when Buddy Strong rips a cord? (f = 440 Hz)

(b) A bottle floating in the ocean bobs up and down once every 2.00 minutes. What is the frequency of this oscillation?

The speed of a computer processor is sometimes indirectly given by stating the frequency at which it electrically oscillates between two states. One such processor is said to operate at 3.1 GHz. What is the period of this processor’s electrical oscillation?

In the above image, you will also notice four important formulas that govern SHM. They describe angular frequency, period, frequency and linear speed of an object in SHM. Let’s put those formulas to the test!!

Walking through Red Rocks, you notice a woodpecker. Now a woodpecker has amazing reinforced skull bones that allow it to peck at a tree without getting a headache!! If you and Jeremy notice that a woodpecker pecks at a tree with a frequency on 22 pecks/second with a peck amplitude of 0.03 m. What is the maximum head speed of this wonderful bird?

Now here’s a tougher one!!

An object of mass 0.80 kg is attached to an ideal horizontal spring that has a spring constant of 180 N/m and is set onto oscillation on a frictionless surface.

(a) Calculate the angular frequency, period and frequency of the block.

(b) Calculate the angular frequency, period and frequency of the mass of the block is quadrupled to 3.2 kg.

ANSWERS!!!

Here are a few more fun SHM questions to polish up your skills!

Paula operates a sewing machine with a needle that moves in SHM as it sees a seam. If the needle moves 8.4 mm from its highest to lowest position and it makes 24 stitches in 9.0 s. What is the maximum needle speed as Paula sees some napkins?

The prong of a tuning fork moves back and forth when it is set into SHM. The distance the prong moves between its extremes positions is 2.24 mm. If the frequency is 440 Hz, what is it’s maximum velocity!

Answers!!

Remember how a spring could be used to store energy. We mentioned this when we talked about the kangaroo hop. The ‘Roo’s tendons act like springs to store spring potential energy, U(spring), which is transformed into kinetic energy when the Roo hops. This observation, along with how a dolphin can swim in an energy efficient manner by utilizing the spring energy in its tail, make it important to look at oscillations from the energy perpspective!

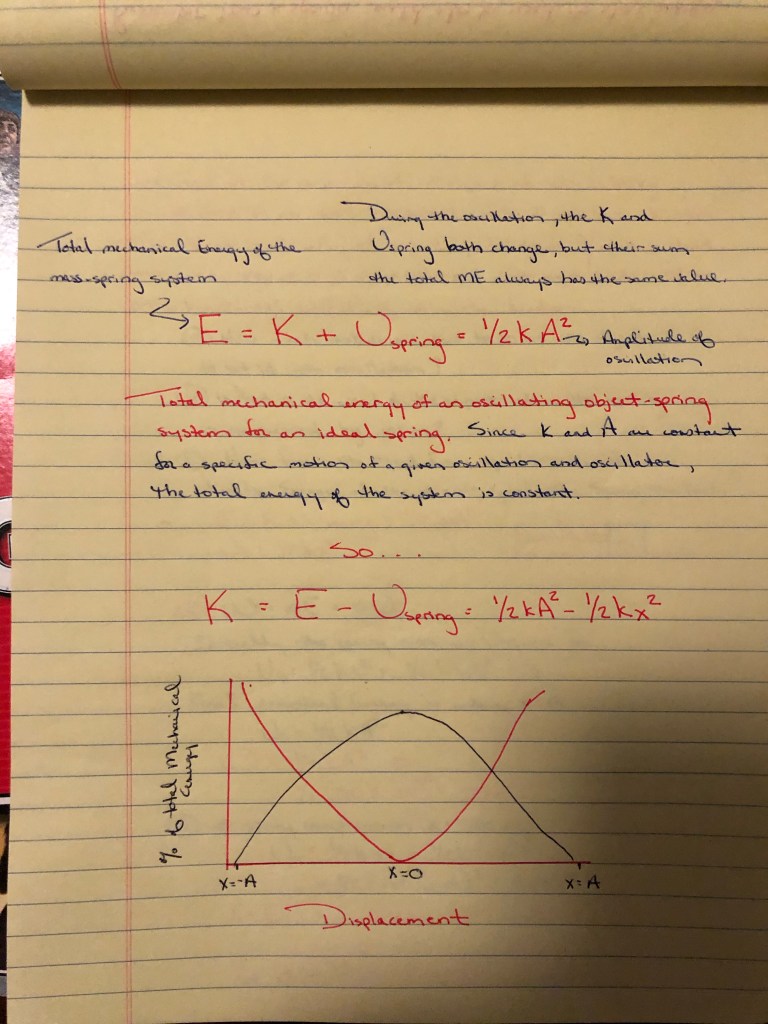
Now, let’s get right into some examples of how we can use Energy to determine position and velocity during an oscillation.

Have any thoughts on this question?

Arthur attaches an object to the end of a spring so it slides back and forth on horizontal surface without friction. The motion is SHM between A and -A. Predict the times at which the object’s K and Us of the system have the same value.

Pendulums!!

I always like to start this unit with a little anecdote!

What do Miley Cyrus and Edgar Allen Poe have in common, besides being great American writers?

The simple pendulum consists of a small object suspended from the end of a lightweight cord. We assume the cord doesn’t stretch and it’s mass can be ignored compared to that of the “bob”. The motion of the simple pendulum back and forth resembles SHM small amplitude oscillations.

The “bob” oscillates along the arc of a circle with equal magnitude on either side of its equilibrium point, or the point where it would hang vertically, where it has its maximum speed! Now we have pendulums everywhere from swingsets to hypnotizing pocket watches. Even our lower leg when we get our reflexes tested can be considered a simple pendulum!!

So we see, just like like with an oscillating spring-mass system, the period (T) of oscillation does not depend on amplitude (angle displaced from vertical) as long as there are small amplitude oscillations. Galileo is said to have first noted this fact whilst watching a swinging lamp in the cathedral of Pisa. The discovery led to the invention of the pendulum clock, the first really precise timepiece, which became the standard for centuries.

Period, frequency and angular frequency are also independent of mass!! Increasing mass increases the inertia but also increases the restoring force, gravity!!

So, if the period of a simple pendulum is T and we increase its length so that it is 4x larger, what will the new period be?

a) T/2 b) T c) 2T d) 4T

1.) A mechanical grandfather clock is driven by the motion of a pendulum, which has a period of a pendulum, which has a period of 2.00 s (and marks the time with each 1.00 s half cycle). What must be the length of pendulum??

2.) A simple pendulum on the surface of Earth is 1.24 m long. What is the angular frequency of the oscillation?

HERE are a couple more questions and the answers!!

Folks!! Here is your QUIZ!!

Thanks everyone!! You are the best!!

The reason the Leaning Tower of Pisa has yet to just topple over is because its Center of Mass (CoM) is still over the base of the tower!! It’s a fascinating concept and one that can lead to several very impressive sculptures, buildings and designs.

The position of the Center of Mass (CoM) of a collection of objects depends on the masses and positions of each individual object. The greater the mass of an object, the greater its impact on the total mass and therefore the greater importance of the object’s position!

xcm = (m1/mt)*x1 + (m2/mt)*x2 …

This formula continues on down until you reach the total (n) number of objects. It basically describes position of the CoM as the sum of the ratios of an object’s mass to the total mass multiplied by the position of the object! You’ll find a couple of examples that we went over here!

If the system, that we are trying to find the CoM for, is in a plane defined by an x and y axis, we need to specify the specific coordinates of the position of the CoM.

There doesn’t have to be any mass at the CoM!! That is, there can be nothing physically at the CoM. The same can be said for any symmetrical object with a hole at its center, like a compact-disc or a donut or ping pong ball. No matter the case, the CoM is located in the center of the empty hole if the mass is distributed evenly.

Now, for motion of the CoM..,

The sum of F(ext) = m(total) x a(CoM)

This tells us that the CoM of a system of objects moves exactly as if the entire mass, m(total), of the system were concentrated at the CoM, and all of the external forces on the system were exerted on that concentrated mass. You can think of the CoM as a tiny blob and all of the external forces are exerted on that blob!!

An exploding cannon shell!!

A civil war reenactment fires a unit of a cannon shell over level ground at a target 200 m away. The cannon is perfectly aimed to hit the target. Air resistance can be neglected. At the highest point of the trajectory, the shell explodes into two identical halves both hitting the ground at the same time. If one falls vertically downward from the explosion. Where does the other half land??

Answer!

Along these lines, let’s have a look at this scenario!!

(1) The CoM of an empty car of 1050 kg is 2.5 m behind the front of the car. How far from the front of the car will the CoM be when two people sit in the front seat 2.8 m from the front of the car and three people sit in the back seat 3.9 m from the front. Assume the mass of each person is 70 kg.

(2) The distance between a Carbon atom (mc = 12 u) and an Oxygen atom (mo = 16 u) molecule is 1.13 x 10^-10 m. How far from the Carbon atom is the CoM?

(3) A 3.0 kg block (A) is attached to a 1.0 kg block (B) by a spring of negligible mass that is compressed and locked in place. The blocks are sliding with negligible friction along the x-direction at initial constant speed of 2.0 m/s.

(a) At time t = 0, the position of block A and B are x = 1.0 m and x = 1.2 m, respectively. Describe the location of the CoM in the mass-spring system at time t = 0.

(b) At the t = 0 a mechanism released the spring and the blocks begging to oscillate as they slide. Predict the location of the CoM 2.0 s later.

(c) If at t = 2.0 s block B is located at 6.0 m, describe the location of block A.

Answers!!

(4) two lumps of clay moving in opposite directions collide with each other and move off as one with no external forces exerted on the system. The first lump has a mass of 0.40 kg and a velocity of 2.0 m/s and the other has a mass of 1.6 kg and a velocity of -1.0 m/s. What is the velocity of the CoM before the collision?

Answer!!

Also here is the test!! Due Friday, 4/17!

Thanks so much for your hard work!!

Angular momentum and its conservation provide the additional information we need to predict the motion of objects in space. It explains the arrangement of solar systems and galaxies. Here on Earth, it explains away the rotation of ocean currents (i.e. The Coriolis Effect), the changing spin of a dancer, diver or skater or the speed and direction of winds in hurricanes and tornadoes, which ultimately leads us to the swirling water in a toilet bowl!!

Angular momentum is always conserved and it is constant when there is zero (0) net torque exerted on the system. This sounds quite similar to linear momentum being constant when there is zero (0) net force exerted on the system. Therefore, we find this rotational equivalent to linear momentum as the angular equivalents of mass times velocity. That is, the moment of inertia times the angular velocity equals angular momentum.

L = Iw

Where L equals angular momentum and I equals the rotational inertia and w equals angular velocity.

This can be seen in the majestic and dazzling jumps and spins in Sasha Cohen’s short program at the Torino Olympic in 2006. This epic routine won her the silver medal in a very crowded field. In this link you will find a quantitative analysis of the basic concept but let’s look at it qualitatively below.

(a) Sasha decreases her moment of inertia, I, by bringing her mass closer to the rotation axis

(b) There are no external torques. Obviously there is an initial torque to send her into a spin but after that the Fg pulls straight down on her CoM, causing zero torque about this axis.

(c) The Fn has no effect for the same reason.

(d) There is negligible torque from her skates.

(e) Angular momentum, L, remains constant therefore, if you decrease the moment of inertia, I, you must increase angular velocity, w.

Napoleon and Deb play Tetherball at the end of the film where they hit ball in opposite directions in an attempt to wrap the ball around the pole. Once, the ball is hit, it has angular momentum around the pole. The angle between r, away from the axis, and F toward the axis is 180 and therefore , t = 0 and angular momentum is conserved. As the rope loops around the pole, its I decreases and its w increases.

But let’s look at some more exciting examples!! Here, we will introduce the concept of a point mass, such as a Phyllis jumping on a stationary merry-go-round to cause it to spin or a mouse on a turntable where I = mR^2. The odd thing to comprehend is that the Phyllis, before jumping on, has an angular momentum, with respect to the rotational axis, even though she is moving linearly. Again here, we have r and F in opposite directions, causing a net torque of zero.

Let’s take a look at some fun problems!!

Phyllis has a mass of 30 kg. She runs toward the merry-go-round at 3.0 m/s, then leaps on! The merry-go-round is initially at rest with a mass of 100 kg and a radius of 2.0 m. The merry-go-round can be considered a uniform disk, I = 1/2 mR^2. Find the angular speed of the merry-go-round after Phyllis jumps on.

Answer!

A disk with a mass of .7 kg and a radius of .15 m is spinning about a vertical axis with angular speed of 9.00 rad/s. A hoop with a mass of 1.0 kg, which initially is not rotating, is dropped vertically on the disk. The two eventually come to rotate at the same speed.

(a) What is the common angular speed of the two objects after the collision?

(b) how much energy is lost to friction in the collision?

Answer!!

Here are a couple of awesome problems!

(1) Mario tosses .5 kg of pizza dough upward and then catches it. During each toss, the dough starts out uniformly distributed and expands. On one toss, the dough has an initial angular speed of 5.20 rad/s, starts as a 20 cm diameter pie and expands to 22 cm in diameter when it’s caught. Assume the mass of the pizza dough remains uniformly distributed. (I = 1/2 mR^2)

(a) Explain why the change in shape of the dough does change the angular speed of the dough but does not change the angular momentum of the dough.

(b) Calculate the angular speed of the dough when Mario catches it.

(2) A pigeon of mass 0.560 kg is flying horizontally at 5.0 m/s and enjoying a nice day. It suddenly runs into a stationary rod and holds on! The rod is uniform, with a length of 0.750 m and a mass of 2.00 kg and is hinged at its base. If the pigeon strikes the rod 0.25 m from the top of the rod, what is the angular velocity of the pigeon-rod system just after the collision? Irod = 1/3 mL^2

Answers to 1 & 2!!!

(3) A 20 kg, uniform board hangs horizontally at rest. It’s left end is connected to a support via a hinge, which is free to rotate. It is also supported by a light rope that makes a 30 degree angle to the board, and which is attached to the board a distance of 3/4 of its length from the hinge. Calculate the tension in the rope.

Answer!!

Here are some additional questions to keep you fresh!

1.) What is the speed of an electron in the lowest energy orbital of hydrogen, of radius equal to 5.29 x 10^-11 m? The mass of an electron is 9.11 x 10^-31 kg and its angular momentum is 1.055 x 10^-34 J s.

2.) A freely moving turntable is rotating at a steady rate when Jeffrey drops a glob of cookie dough and it attaches to the very edge of the turntable. Describe which quantities – angular velocity, angular acceleration, torque, Rotational KE, rotational inertia or angular momentum– are constant during the process. If the property changes, predict whether it increases or decreases.

3.) A 1000 kg merry-go-round is spinning, while supporting 10 acrobats, each with a mass of 50 kg. Initially the acrobats support each other to form a column very close to the axis of rotation (thus, the acrobats have no angular momentum at this location). Describe a plan to move the acrobats such that the angular velocity of the merry-go-round decreases to half its initial value.

4.) A disk of mass Is M and radius R has a rocket motor attached to its edge. Assume the rocket motor has negligible mass compared to the disk. The disk is free to rotate with negligible friction about and axis through its CoM perpendicular to the disk. The rocket motor fires, causing the disk to begin to rotate about this axis. The rocket, while it is firing, provides a constant force, Fo, tangent to the disk, for a time t. I = 1/2mR^2.

(a) Derive an expression for change in angular momentum of the disk in terms of the given quantities and physics constants.

(b) Derive an expression for the angular speed of the disk after the rocket has fired. Give the answer in terms of given quantities and fundamentals constants.

The rocket motor has now been adjusted so that it is angled to the edge of the disk, pointed inward. Assume the rocket fires for the same amount of time and applies a force of the same magnitude.

(c) how does the final angular speed of the disk compare to the answer you found in part (b)?

Answers!!!

OK!! Here is the TEST!!

A lawnmower starter is a flywheel and a great example of our learned ability to manipulate torque!

Simply opening a door can tell us so much! We have the door handle as far away from the hinges as possible and we want to push perpendicular to the plane of the door. This is a great model as to how giving an extended object angular acceleration is not only dependent on how hard you push but also where and in what direction you push. The physical quantity that relates all of these aspects of an applied force is called the torque associated with said force. In perfect harmony with Newton’s 2nd Law, the net external torque determines the angular acceleration just as net force determines linear acceleration!!

So, we use r to denote the vector from the rotation axis to the point where the force is applied and we use the symbol (phi or theta) for the angle between the directions of r and F. It is the perpendicular component of the this force that makes the object rotate, F sin (theta). This is torque!!

Torque (tau) = rF sin (theta)

…where r is the distance from the rotation axis to where the force is applied and theta is the angle between the vector r (from the axis to where the force is applied) and the force vector F.

Torque has direction in terms of clockwise (-) and counterclockwise (+). In the photo above, part (c) shows the “line of action” of the force as the extension of the force vector through the point where the force is applied. The lever arm or moment arm is the perpendicular distance from the rotation axis to the line of action of the force, r (perpendicular) = r sin (theta) and we are left with same quantity as before.

tau = r (perpendicular) F

r (perpendicular) represents the lever arm! So the longer the lever arm, the greater the torque for a given amount of force! So even a small force can generate a large torque of the lever arm is long enough!

Now that we have a general knowledge of torque, let’s have a go at a few problems!!

(1) Marcy can deliver about 10 Nm of torque when attempting to open a twist off cap on an Orange Crush soda bottle. What is the maximum force Marcy can exert with her fingers if the bottle cap’s diameter in 2 cm?

(2) Bettina Henderson applies a horizontal force of 20 N (to the right) to the top of a steering wheel on the way to soccer practice. The wheel had a radius of 18 cm and a Rotational Inertia of .097 kgm^2. Calculate the angular acceleration about the central axis due to the force.

(3) Many 6.35 cm-diameter computer hard disks spin a t a constant 7200 rpm operating speed. The disk’s have a mass of about 7.50 g and are essentially uniform throughout with a small hole in the center. I = 1/2mr^2.

(a) if the disk reaches its operating speed 2.50 s after the drive is turned on, what average torque does the drive supply to the disk during the acceleration?

(b) calculate the change in Kinetic Energy of the disk and the average power delivered to the drive as it accelerated to operating speed.

Answers!!

(4) A block of mass m1 = 2.00 kg rests on a table that exerts a negligible friction force on the block. The block is connected with a light string over a pulley to a hanging mass m2 = 4.00 kg. The pulley is a uniform disk with a radius of 4.00 cm and a mass of .500 kg. The rotational inertia of a uniform disk is 1/2mr^2.

(a) Calculate the acceleration of each block and the tension in each segment of the string.

(b) Calculate how long it takes the blocks to move a distance of 2.25 m.

(c) Calculate the angular speed of the pulley at the instant the blocks are moved.

Answer!!

Here are a couple for home!!

(1) Shawna, a 45 kg high diver, launches herself from a springboard that is 3.0 m above the water’s surface, so that she ends up with a 5.0 m fall from rest before she reaches the surface of the water. Calculate the time it takes Shawna to descend the 5 m to the surface of the water and the angular speed that will allow Shawna to complete 2.5 turns while in the air!

(2) Sarah’s potter wheel is mounted on a shaft with bearings that exert a negligible friction force, the wheel is initially at rest. A constant external torque of 75 Nm is applied to a wheel for 15 s, giving the wheel an angular speed of 500 rpm in the counterclockwise direction when viewed from above.

(a) Calculate the magnitude of the angular acceleration of the wheel in rad/s^2. What is its direction?

(b) Express the rotational inertia of the wheel in terms of the torque exerted on the wheel and the angular acceleration of the wheel.

(c) calculate the value of the rotational inertia of the wheel.

(d) The external torque is removed and a brake applied. If it takes the wheel 200 s to come to rest after the brake is applied, what is the magnitude and direction of the torque exerted on the brake?

Answers!!

OK! So, here is the answers for the cart/wheel worksheet from last week and here is a new wheels worksheet along with the answers!!!

Here is another problem with its solution, of a tension force rotating a cylinder. I also wanted to add the solution to the torque ruler scenario we went over before we left school.

I know this is a lot but it is basically all of torque. We will be here for a little bit.

Thanks so much everybody!! You all are incredible!!!