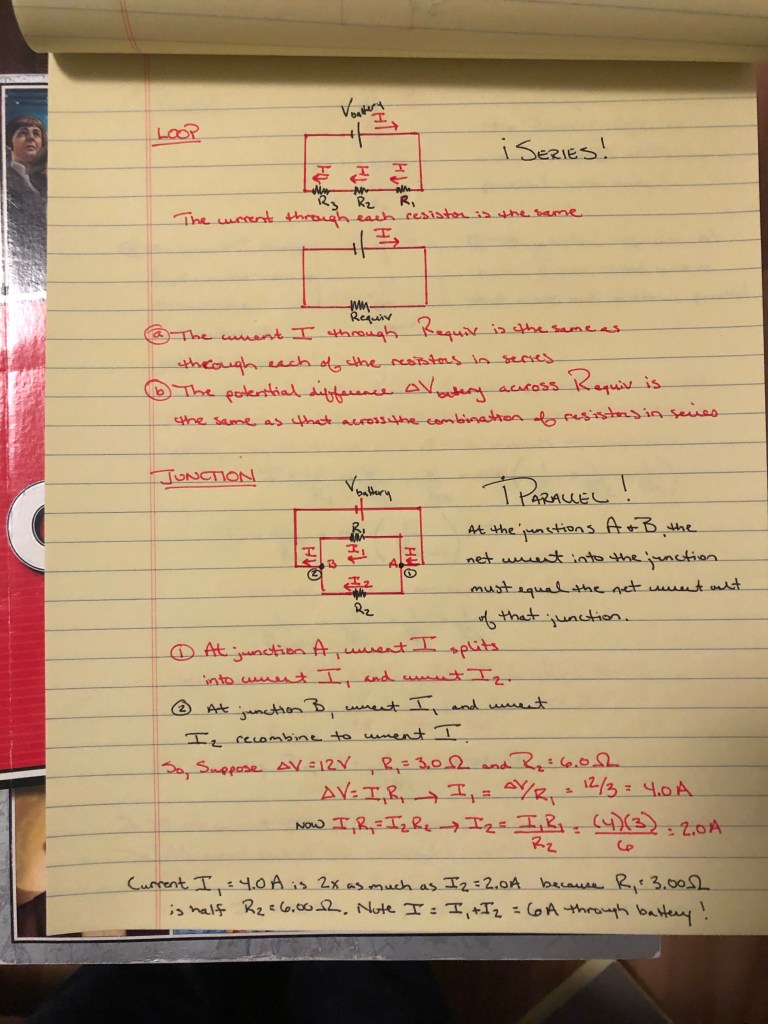
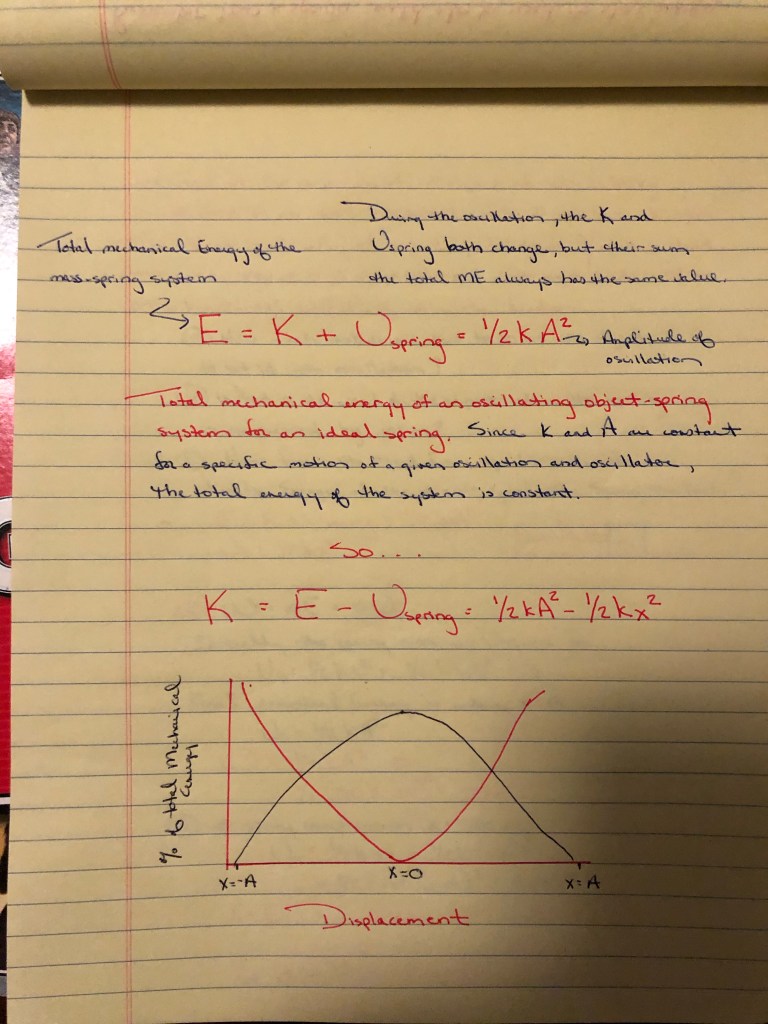
A point on the outside of a turntable moves a greater distance in one complete rotation than a corresponding point on the inside. If something moves a greater distance in the same time, this means a greater speed. So the linear or tangential speed is greater on the outside of a rotating object than inside and closer to the axis. This is still denoted with a v and is measured in m/s.

Angular speed, denoted by w, refers to the number of revolutions per unit time. Since all parts of the turntable rotate about the axis in the same amount of time, all parts have the same number of revolutions per unit time. That is, they “sweep” out the same angle no matter their distance from the axis! The angular speed is usually expressed in RPM and for analysis we like to convert it to rad/s as w is also equal to change (theta)/time, using this conversion factor.

2(pi) radians/revolution

Tangential speed and rotational speed are directly related by the formula

v = wr

Angular Speed of a DVD!!

On a DVD, visual and audio data are stored in a series of tiny pits that are evenly spaced along a long spiral that spans most of the surface of the disk and extends from the inner edge to the outer edge. The scanning laser in a DVD player reads the information at a constant rate. As the player reads closer and closer to the outer edge of the DVD, should the disk rotate…

(a) faster (b) slower (c) the same speed

In order to read the info at a constant rate, the same linear distance along the spiral must pass the reader in a given rate of time, regardless of radius. Distance in this case is the length of the circular arc, which is given be r((delta)(theta)). In order for this to remain constant, as r increases the angular displacement (change(theta)), in any fixed amount of time, (w), must decrease, v = wr, So as the scanning laser gets closer to the edge, the angular speed must decrease! The answer is (b).

So, at the end of the day, tangential speed is directly proportional to both angular speed and radius!

Rotational Inertia!!

The property of an object to resist changes in its rotational state of motion is called rotational inertia. This is the rotational equivalent to mass. An object rotating about an axis tends to remain rotating unless acted upon by an external torque, the rotational equivalent to force.

Rotational inertia, I, depends on the distribution, of mass around the axis of rotation. The further the the distribution of the mass from the axis, the greater the rotational inertia, I. The greater the I, the harder it is to change the state of rotation of the object.

The rotational inertia of any object depends on the mass distribution around its axis. A pencil can be rotated around three (3) different axes and therefore has three different rotational inertias. Sometimes a player will choke up on the baseball bat with 2 strikes in order to protect the plate. Why do you think they do this in terms of rotational inertia? Besides Barry Bonds, has a power hitter ever choked up on the bat?

How should you balance a hammer on your finger?

HERE is a super fun way to to analyze rotational motion down a ramp!!

Torque!!

This arm wrestling video and subsequent diagram and input is a really fun way to look at torque!

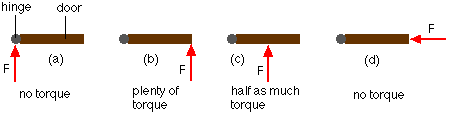
In its simplest, we can look at torque through an open door. By this, I mean, where and in what direction should we push or pull on a door to give the most angular acceleration around its hinges? What does experience tell you? Have a think?

Torque is simply force at a distance. That is, the force multiplied by its distance from the axis of rotation. The angle between the force vector and the radial vector, from the axis to the point of application of the force is perpendicular component of the force, Fsin(theta). This component makes the object rotate and is maximized at the perpendicular, or 90 degrees where sin(90) = 1!

Torque has direction, in terms of clockwise (CW) and counterclockwise (CCW). CCW is seen as the positive direction.

The “Line of Action” of this force is the extension of the force vector through the point where the force is exerted. The Lever Arm or Moment Arm, as we saw in the arm wrestling video, is the perpendicular distance form the rotation axis to the line of action of the force. See below.

Torque (tau) = F x r (sin(theta))

…or…

Torque (tau) = F x r(perpendicular)

Torque is also the rotational equivalent of force!! So we can also express the sum of the torques relating to our favorite formula.

Sum (torques) = I (alpha)

The Rotational Equivalent to Newton’s 2nd Law!!

The ability to set these equations equal to each other allows us to analyze rotational motion problem from several aspects and we will get into this in a little bit!

Theresa holds a 10 kg kettle ball in one hand at arm,s length and at shoulder height. Assuming her hand is 75 cm from her shoulder and neglect any torque caused by the weight of your arm, what is the torque about Theresa’s shoulder axis?

Angular Momentum!!!

Just like linear momentum, angular momentum is constant when there are no external torques exerted on the system!! So just like our formula for torque, angular momentum expresses the rotational equivalents of linear momentum.

L = Iw

The interesting this bit about angular momentum is, that, if an object is traveling in linear motion, it has angular momentum with respect to the the axis of rotation it’s about to collide with!! The formula for the initial angular momentum of a point mass in linear motion is represented below.

L = mvr

Just as in linear momentum, the angular momentum before the collision can be set equal to the angular momentum after the collision if there are no external torques.

Iw(before) = Iw(after)

🍕 This wonderful relationship solves the mystery of the pizza toss!! 🍕

HERE are some fantastic wrap up questions for this unit!!

DC Circuits: Electric charge in motion!

So many situations in nature and technology involve electric charge in motion. The movement of electric charge along the optic nerve from your eye to your visual cortex transmits the image of a turtle in the form of a coded electric signal. If it’s nighttime, you’re reading your iPad that operates by using very complex electric circuitry. Or you can use the simplest circuit, a battery connected to a lightbulb to illuminate the room and allow you to read Harry Potter. The battery causes electrons to move through the circuit. As these electrons move through the lightbulb, they transfer energy in order to make it shine!

So we will briefly look at the Physics of electric charge in motion! A current measures the rate at which charge moves through a conductor. Ordinary conductors have resistance to the motion of charge so we set up a change is potential energy between the ends of a conductor to produce this motion, voltage. Just like a block siding down a ramp when friction is involved! In circuits, the increase in potential energy is the source of an emf (electromotive force) with the most common form being the battery. Simple circuits involve a battery and one or more resistors. I’m it’s purest, an electric circuit is used to transfer energy from on place to another.

DYK? A bolt of lightning releases so much energy that it heats air to a temperature of 30000 degrees Celsius, stripping electrons from atoms causing the air to glow!! Some specialized species of fish, like electric rays are equipped with organic batteries that can unleash a burst of energy to stun prey or fend off predators!

Electric Current is equal to the rate at which current moves!

So a battery sets electric charge carriers, electrons, in motion. A battery contains one or more electrochemical cells. Inside the cell are two different substances that, due to their different chemical properties undergo a chemical reaction so that each substance ends up with an excess or deficit of electrons. In the common battery, zinc ends up with the electron excess, manganese dioxide ends up with the deficit.

The terminals of a battery are each connected to one of the substances and electrons move between each substance. The terminal with the electron excess is the negative terminal and the terminal with electron deficit is the positive terminal. Because of the charge differential, the positive terminal has the higher electric potential. The potential depends on the substances and, for the aforementioned, it’s 1.5 V. A 9-Volt battery is made up of six 1.5 V cells.

In a closed circuit, where the wire makes up a complete loop, charge moves continuously from one terminal to another as if it were an object sliding down a ramp with friction near the Earth’s surface. Inside the battery, the chemical reaction “lifts” the charge back up to the top of the incline!

Current!!

Just like river, an electrons flow like water and an electric current is equal to the rate at which charge moves past any point in the circuit.

I = change (charge)/change (time)

The unit of current is the Ampere and 1 Ampere is equal to 1 Coulomb/s. We will say that the current has the same value at all times. This means electrons cannot “pile up” at any point except the terminals. Since charge is conserved, there is also no way for for more moving charged objects to join the current or for charged objects to leave the current. Whatever the amount of charge that moves into a point in the circuit, the same amount of charge must move out of the same point. The values of the current is the same around a closed loop! Current is not a vector but it does have direction, which is associated with which way positive charge would flow!

Resistance!!!

Electrical resistance can be found in every technological device, from the wires in an automobile ignition system to the resistors in a computer or mobile phone. What purpose does resistance serve? Well, the greater the resistance, the smaller the current, I. The resistance allows us to control the current due to any particular applied electric potential difference.

Resistivity, rho, depends on the material of which a wire is made a tells how well or poorly this material inhibits the flow of electric charge. For a copper wire, a good conductor of electricity, the resistivity is very low. For rubber, resistivity is high which makes rubber a poor conductor but a great insulator. Resistivity increases with temperature as heating increases disorganization and therefore collisions with electrons.

R = rho(L)/A

Ohm’s Law

Change (V) = IR

For a constant potential difference, such as a battery, across a resistor in a closed loop, the current will be the same everywhere in the loop. If you change the value of the resistance, then the amount of current will change compared to the original circuit but the current will still be the same everywhere in the loop!

We see this in every one of our cells!! In order for a cell to live, there must be a higher concentration of positively charged K+ ions inside the cell than outside the cell. This difference in concentration mean that K+ ions will leak out through potassium channels. This flow of K+ constitutes a current and the channel acts like a resistor. The movement of K+ through the membrane of your cells is determined by the electrical resistance of the membrane channels!

HERE are a few problems!!

Circuits!!

Once a current is established, the change in energy of a charge as it moves around a closed path must add to zero. And, as we learned, the electric potential difference is the change in energy per unit charge. This idea was first brought to bare by Prussian physicist, Gustav Kirchhoff and is called Kirchhoff’s Loop Rule:

The sum of the changes in potential around a closed loop in a circuit must equal zero.

An important application of The Loop Rule is to resisters in series, that is, resistors connected end to end. The total energy given to a charge as it moves through the battery must be equal to the energy it loses through the resistors, no matter the number of resistors. Let’s say we replace three resistors in a circuit with an equivalent resistance that gives the same current as the series combination. So, according to Ohm’s Law, the same current is present through each of the resistors and the total change in potential (V) across three resistors in series is the sum of the voltage differences.

IR(equiv) = IR(1) + IR(2) + IR(3)

…and this simplified to…

R(equiv) = R(1) + R(2) + R(3)

Combining resistors in series creates a circuit with a higher equivalent resistance than that of any individual resistor! Essentially we have made a longer resistor by placing resistors “end to end“. For resistors in series, the current is the same through each resistor but the change(V) is different for different resistors. (V = IR)

Unlike a single loop, resistors in parallel constitute a multi-loop circuit and make up most household circuits! There is more than one pathway that the moving charge can take through the circuit from the positive terminal to the negative terminal. In the example below, there are two two junctions where the currents either breaks or comes together. What is the relationship between current I that passes through the battery, I(1) that goes through R(1) and I(2) that goes through R(2)?

Well, since charge is always conserved, the current is conserved which means that charge can neither be created nor destroyed, nor pile up. The rate at which the current arrives at a junction must equal the rate at which the charge leaves the junction. This is Kirchhoff’s Junction Rule.

The sum of the currents into a junction equals the sum of the currents out of the junction.

Let’s apply the Junction Rule to the circuit below. The current I represents the flow of charge into Junction A and current I(1) and I(2) represent the charge flow out of it. Therefore, I = I(1) + I(2). At Junction B, the sum of the currents in is I(1) + I(2) and the sole current out is I. So if we look at each junction, I = I(1) + I(2). The currents divide and rejoin at junctions A & B, respectively!

This concept, neat for sure, doesn’t tell us how much of I takes the branch into R(1) as I(1) and how much takes the branch through resistor R(2) as I(2). To determine this, let’s apply the Loop Rule to two different loops!

First, consider the loop that starts at the negative terminal and travel through the battery to the positive terminal (electric potential increases by V(battery)) then follows I(1) through R(1) and the electric potential decreases by I(1)R(2) and returns to the negative terminal. From the loop, the net change in electric potential is zero so…

change(V(battery)) = I(1)R(1)

The second loop starts in the same manner and then follows the path of I(2) through R(2). Again the Loop Rule states that the net change is zero so…

change(V(battery)) = I(2)R(2)

These equations can only be true if

I(1)R(1) = I(2)R(2)

In other words, for resistors in parallel, the electric potential must be the same for each resistor. However, the currents are different for each resistor.

If R(1) is less than R(2) the current will be greater in R(1) and smaller in R(2).

So, as you can see, the current is greatest through R(2) which has the smallest of the the three resistances. So combining resistors in parallel creates a circuit with a smaller equivalent resistance than any of the individual resistors. We have, essentially, increased the cross-sectional area of the equivalent resistor!!

Power!!

The transfer of energy, like from the wall socket to your toaster or tea kettle is the most fundamental use of an electric circuit. And, we mostly are concerned with the rate at which this energy is transferred in or out of the circuit element. After all, we want our bagel in a minute or two, not an hour, am I right??

Power is the rate at which energy is transferred. Every single lightbulb is stamped with the amount of powers that must be supplied to it. So, with a current I in a circuit, the power P for each circuit element is simply the rate at which electric potential energy is converted by that element. So…

P = change(q)/change(t) x V

…or…

P = IV

And since V = IR

P = I^2R and P = V^2/R

So in it’s purest form, a household lightbulb is designed to be connected to the standard 120 V parallel circuit at Flynn Ave. as opposed to the 240 V parallel circuits on Abbey Rd. So assuming a supply of 120 each bulb is rated a different wattage. A 40 W bulb dissipates 40 W only if it is supplied with 120 V. A 100 W bulbs dissipates energy faster and thus the bulb is brighter!! Also, Burlington Electric charges us based not on the power we use but the total energy we use. Since P = change(E)/time, the units of Energy are the units of power multiplied by the unit of time. Hence we see Kilowatt(hours) on our bill!!

And HERE we have a few awesome problems!!

And THIS worksheet will be very helpful if you wanted to have some fun with it. It’s kind of like a puzzle.

…and finally here is the key to the worksheet above!! It is such a great exercise and so important to understanding circuits!!!

Your nearly one stop shop for review!!

The AP Daily Live Reviews from College Board are AWESOME!!!

The videos from Flipping Physics are the best way to review for the exam!!!

I’ve put together a DCS (Our year on a Sheet)!

AP Physics 1 Equation Sheet!!!

This is where you will find the answers to some useful Rotational scenarios!!

Have a look at the key for last year’s Rotation test!!

Here is where I will be posting answers to FRQs that we will be going over during class.

1.) The Diver!!

2.) The Ferris Wheel!!!

3.) The Three Pulleys!!

4.) The Rocket Launcher!!

5.) The Astronaut!!

6.) The Cliff!!

7.) The Blocks!!!

Check THIS out for a quick review of Atwood and Modified Atwood systems!!

8.) The Stars!!

9.) The Asteroids!!!

10.) The Ramp using Work!!

11.) The Rockets using work!!

12.) The Impulse!!

13.) The BLOCK up the ramp (force)!!

🍿Important Style Example!! 🥐

The Bumpy Ramp!!!

14.) The Pipe/Spin problem!!

15.) The Ramp Collision!!!

16.) The BeeBee CHANGE IN MOMENTUM!!

🍋 REVIEW SESSION 🍎

The Long QQT!!!

The Two Carts in opposite directions!!

The other Disk/Rod concept!!

The Curved Track for momentum and energy!!

The Free Fall or Push Kinematics concepts!!

The Pendulum Kinematics and Energy and Momentum Combo! This example has calculations but it is supremely relevant!

The Roller Coaster!!!

We live in a world of oscillations!! You can try keeping your body absolutely still but your heart will still beat and your lungs will still expand and relax. All the while, electrons move back and forth about 60 times/sec as part of the process to supply energy to the LCD screeen on your iPhone!

Oscillations are characterized as movement of an object back and forth around a specific point of equilibrium, that is, a point of zero force. Oscillations have a cycle, occurring as a repeating pattern. The time for one complete cycle is called the Period (T) of an oscillation.

The cyclic appearance of Venus proved Copernicus’ sun centric solar system!

The simplest form of oscillation occurs when the restoring force obey’s Hooke’s Law. That is, when the restoring force is directly proportional to the distance that the oscillating object is displaced from equilibrium. This is called an Ideal Spring.

F = -kx

The negative sign indicates that the force is always opposite the displacement.

Shelly exerts a force of 10 N on a spring, stretching it a distance of 20 cm.

(a) How far will the spring stretch if a force of 20 N is exerted on it?

(b) What is the spring constant of the spring?

Please enjoy the amazing Trey Anastasio manipulating SHM.

We know the Period (T) is the time it takes to complete one cycle in SHM. Frequency (f) is equal to the number of oscillations per unit time. We usually assign the unit Hertz (Hz) to frequency that basically means “anything per second”.

Since (T) is the number of seconds elapsed per cycle and (f) is the total number of cycles per second, it stands to reason that these quantities are reciprocals. This is very useful!

f = 1/T and T = 1/f

Farrah has a resting heart rate of 50 beats/min. When Farrah sprints a lap on the track, her pulse increases to 150 bpm. Compared to when she is at rest, the period of her heart rate when she is sprinting is

(a) 9x (b) 3x (c) same (d) 1/3x (e) 1/9x

(a) What is the oscillation period of your eardrum when you are listening to the A4 note on the piano when Buddy Strong rips a cord? (f = 440 Hz)

(b) A bottle floating in the ocean bobs up and down once every 2.00 minutes. What is the frequency of this oscillation?

The speed of a computer processor is sometimes indirectly given by stating the frequency at which it electrically oscillates between two states. One such processor is said to operate at 3.1 GHz. What is the period of this processor’s electrical oscillation?

In the above image, you will also notice four important formulas that govern SHM. They describe angular frequency, period, frequency and linear speed of an object in SHM. Let’s put those formulas to the test!!

Walking through Red Rocks, you notice a woodpecker. Now a woodpecker has amazing reinforced skull bones that allow it to peck at a tree without getting a headache!! If you and Jeremy notice that a woodpecker pecks at a tree with a frequency on 22 pecks/second with a peck amplitude of 0.03 m. What is the maximum head speed of this wonderful bird?

Now here’s a tougher one!!

An object of mass 0.80 kg is attached to an ideal horizontal spring that has a spring constant of 180 N/m and is set onto oscillation on a frictionless surface.

(a) Calculate the angular frequency, period and frequency of the block.

(b) Calculate the angular frequency, period and frequency of the mass of the block is quadrupled to 3.2 kg.

ANSWERS!!!

Here are a few more fun SHM questions to polish up your skills!

Paula operates a sewing machine with a needle that moves in SHM as it sees a seam. If the needle moves 8.4 mm from its highest to lowest position and it makes 24 stitches in 9.0 s. What is the maximum needle speed as Paula sees some napkins?

The prong of a tuning fork moves back and forth when it is set into SHM. The distance the prong moves between its extremes positions is 2.24 mm. If the frequency is 440 Hz, what is it’s maximum velocity!

Answers!!

Remember how a spring could be used to store energy. We mentioned this when we talked about the kangaroo hop. The ‘Roo’s tendons act like springs to store spring potential energy, U(spring), which is transformed into kinetic energy when the Roo hops. This observation, along with how a dolphin can swim in an energy efficient manner by utilizing the spring energy in its tail, make it important to look at oscillations from the energy perpspective!

Now, let’s get right into some examples of how we can use Energy to determine position and velocity during an oscillation.

Have any thoughts on this question?

Arthur attaches an object to the end of a spring so it slides back and forth on horizontal surface without friction. The motion is SHM between A and -A. Predict the times at which the object’s K and Us of the system have the same value.

Pendulums!!

I always like to start this unit with a little anecdote!

What do Miley Cyrus and Edgar Allen Poe have in common, besides being great American writers?

The simple pendulum consists of a small object suspended from the end of a lightweight cord. We assume the cord doesn’t stretch and it’s mass can be ignored compared to that of the “bob”. The motion of the simple pendulum back and forth resembles SHM small amplitude oscillations.

The “bob” oscillates along the arc of a circle with equal magnitude on either side of its equilibrium point, or the point where it would hang vertically, where it has its maximum speed! Now we have pendulums everywhere from swingsets to hypnotizing pocket watches. Even our lower leg when we get our reflexes tested can be considered a simple pendulum!!

So we see, just like like with an oscillating spring-mass system, the period (T) of oscillation does not depend on amplitude (angle displaced from vertical) as long as there are small amplitude oscillations. Galileo is said to have first noted this fact whilst watching a swinging lamp in the cathedral of Pisa. The discovery led to the invention of the pendulum clock, the first really precise timepiece, which became the standard for centuries.

Period, frequency and angular frequency are also independent of mass!! Increasing mass increases the inertia but also increases the restoring force, gravity!!

So, if the period of a simple pendulum is T and we increase its length so that it is 4x larger, what will the new period be?

a) T/2 b) T c) 2T d) 4T

1.) A mechanical grandfather clock is driven by the motion of a pendulum, which has a period of a pendulum, which has a period of 2.00 s (and marks the time with each 1.00 s half cycle). What must be the length of pendulum??

2.) A simple pendulum on the surface of Earth is 1.24 m long. What is the angular frequency of the oscillation?

HERE are a couple more questions and the answers!!

Folks!! Here is your QUIZ!!

Thanks everyone!! You are the best!!

The reason the Leaning Tower of Pisa has yet to just topple over is because its Center of Mass (CoM) is still over the base of the tower!! It’s a fascinating concept and one that can lead to several very impressive sculptures, buildings and designs.

The position of the Center of Mass (CoM) of a collection of objects depends on the masses and positions of each individual object. The greater the mass of an object, the greater its impact on the total mass and therefore the greater importance of the object’s position!

xcm = (m1/mt)*x1 + (m2/mt)*x2 …

This formula continues on down until you reach the total (n) number of objects. It basically describes position of the CoM as the sum of the ratios of an object’s mass to the total mass multiplied by the position of the object! You’ll find a couple of examples that we went over here!

If the system, that we are trying to find the CoM for, is in a plane defined by an x and y axis, we need to specify the specific coordinates of the position of the CoM.

There doesn’t have to be any mass at the CoM!! That is, there can be nothing physically at the CoM. The same can be said for any symmetrical object with a hole at its center, like a compact-disc or a donut or ping pong ball. No matter the case, the CoM is located in the center of the empty hole if the mass is distributed evenly.

Now, for motion of the CoM..,

The sum of F(ext) = m(total) x a(CoM)

This tells us that the CoM of a system of objects moves exactly as if the entire mass, m(total), of the system were concentrated at the CoM, and all of the external forces on the system were exerted on that concentrated mass. You can think of the CoM as a tiny blob and all of the external forces are exerted on that blob!!

An exploding cannon shell!!

A civil war reenactment fires a unit of a cannon shell over level ground at a target 200 m away. The cannon is perfectly aimed to hit the target. Air resistance can be neglected. At the highest point of the trajectory, the shell explodes into two identical halves both hitting the ground at the same time. If one falls vertically downward from the explosion. Where does the other half land??

Answer!

Along these lines, let’s have a look at this scenario!!

(1) The CoM of an empty car of 1050 kg is 2.5 m behind the front of the car. How far from the front of the car will the CoM be when two people sit in the front seat 2.8 m from the front of the car and three people sit in the back seat 3.9 m from the front. Assume the mass of each person is 70 kg.

(2) The distance between a Carbon atom (mc = 12 u) and an Oxygen atom (mo = 16 u) molecule is 1.13 x 10^-10 m. How far from the Carbon atom is the CoM?

(3) A 3.0 kg block (A) is attached to a 1.0 kg block (B) by a spring of negligible mass that is compressed and locked in place. The blocks are sliding with negligible friction along the x-direction at initial constant speed of 2.0 m/s.

(a) At time t = 0, the position of block A and B are x = 1.0 m and x = 1.2 m, respectively. Describe the location of the CoM in the mass-spring system at time t = 0.

(b) At the t = 0 a mechanism released the spring and the blocks begging to oscillate as they slide. Predict the location of the CoM 2.0 s later.

(c) If at t = 2.0 s block B is located at 6.0 m, describe the location of block A.

Answers!!

(4) two lumps of clay moving in opposite directions collide with each other and move off as one with no external forces exerted on the system. The first lump has a mass of 0.40 kg and a velocity of 2.0 m/s and the other has a mass of 1.6 kg and a velocity of -1.0 m/s. What is the velocity of the CoM before the collision?

Answer!!

Also here is the test!! Due Friday, 4/17!

Thanks so much for your hard work!!

Angular momentum and its conservation provide the additional information we need to predict the motion of objects in space. It explains the arrangement of solar systems and galaxies. Here on Earth, it explains away the rotation of ocean currents (i.e. The Coriolis Effect), the changing spin of a dancer, diver or skater or the speed and direction of winds in hurricanes and tornadoes, which ultimately leads us to the swirling water in a toilet bowl!!

Angular momentum is always conserved and it is constant when there is zero (0) net torque exerted on the system. This sounds quite similar to linear momentum being constant when there is zero (0) net force exerted on the system. Therefore, we find this rotational equivalent to linear momentum as the angular equivalents of mass times velocity. That is, the moment of inertia times the angular velocity equals angular momentum.

L = Iw

Where L equals angular momentum and I equals the rotational inertia and w equals angular velocity.

This can be seen in the majestic and dazzling jumps and spins in Sasha Cohen’s short program at the Torino Olympic in 2006. This epic routine won her the silver medal in a very crowded field. In this link you will find a quantitative analysis of the basic concept but let’s look at it qualitatively below.

(a) Sasha decreases her moment of inertia, I, by bringing her mass closer to the rotation axis

(b) There are no external torques. Obviously there is an initial torque to send her into a spin but after that the Fg pulls straight down on her CoM, causing zero torque about this axis.

(c) The Fn has no effect for the same reason.

(d) There is negligible torque from her skates.

(e) Angular momentum, L, remains constant therefore, if you decrease the moment of inertia, I, you must increase angular velocity, w.

Napoleon and Deb play Tetherball at the end of the film where they hit ball in opposite directions in an attempt to wrap the ball around the pole. Once, the ball is hit, it has angular momentum around the pole. The angle between r, away from the axis, and F toward the axis is 180 and therefore , t = 0 and angular momentum is conserved. As the rope loops around the pole, its I decreases and its w increases.

But let’s look at some more exciting examples!! Here, we will introduce the concept of a point mass, such as a Phyllis jumping on a stationary merry-go-round to cause it to spin or a mouse on a turntable where I = mR^2. The odd thing to comprehend is that the Phyllis, before jumping on, has an angular momentum, with respect to the rotational axis, even though she is moving linearly. Again here, we have r and F in opposite directions, causing a net torque of zero.

Let’s take a look at some fun problems!!

Phyllis has a mass of 30 kg. She runs toward the merry-go-round at 3.0 m/s, then leaps on! The merry-go-round is initially at rest with a mass of 100 kg and a radius of 2.0 m. The merry-go-round can be considered a uniform disk, I = 1/2 mR^2. Find the angular speed of the merry-go-round after Phyllis jumps on.

Answer!

A disk with a mass of .7 kg and a radius of .15 m is spinning about a vertical axis with angular speed of 9.00 rad/s. A hoop with a mass of 1.0 kg, which initially is not rotating, is dropped vertically on the disk. The two eventually come to rotate at the same speed.

(a) What is the common angular speed of the two objects after the collision?

(b) how much energy is lost to friction in the collision?

Answer!!

Here are a couple of awesome problems!

(1) Mario tosses .5 kg of pizza dough upward and then catches it. During each toss, the dough starts out uniformly distributed and expands. On one toss, the dough has an initial angular speed of 5.20 rad/s, starts as a 20 cm diameter pie and expands to 22 cm in diameter when it’s caught. Assume the mass of the pizza dough remains uniformly distributed. (I = 1/2 mR^2)

(a) Explain why the change in shape of the dough does change the angular speed of the dough but does not change the angular momentum of the dough.

(b) Calculate the angular speed of the dough when Mario catches it.

(2) A pigeon of mass 0.560 kg is flying horizontally at 5.0 m/s and enjoying a nice day. It suddenly runs into a stationary rod and holds on! The rod is uniform, with a length of 0.750 m and a mass of 2.00 kg and is hinged at its base. If the pigeon strikes the rod 0.25 m from the top of the rod, what is the angular velocity of the pigeon-rod system just after the collision? Irod = 1/3 mL^2

Answers to 1 & 2!!!

(3) A 20 kg, uniform board hangs horizontally at rest. It’s left end is connected to a support via a hinge, which is free to rotate. It is also supported by a light rope that makes a 30 degree angle to the board, and which is attached to the board a distance of 3/4 of its length from the hinge. Calculate the tension in the rope.

Answer!!

Here are some additional questions to keep you fresh!

1.) What is the speed of an electron in the lowest energy orbital of hydrogen, of radius equal to 5.29 x 10^-11 m? The mass of an electron is 9.11 x 10^-31 kg and its angular momentum is 1.055 x 10^-34 J s.

2.) A freely moving turntable is rotating at a steady rate when Jeffrey drops a glob of cookie dough and it attaches to the very edge of the turntable. Describe which quantities – angular velocity, angular acceleration, torque, Rotational KE, rotational inertia or angular momentum– are constant during the process. If the property changes, predict whether it increases or decreases.

3.) A 1000 kg merry-go-round is spinning, while supporting 10 acrobats, each with a mass of 50 kg. Initially the acrobats support each other to form a column very close to the axis of rotation (thus, the acrobats have no angular momentum at this location). Describe a plan to move the acrobats such that the angular velocity of the merry-go-round decreases to half its initial value.

4.) A disk of mass Is M and radius R has a rocket motor attached to its edge. Assume the rocket motor has negligible mass compared to the disk. The disk is free to rotate with negligible friction about and axis through its CoM perpendicular to the disk. The rocket motor fires, causing the disk to begin to rotate about this axis. The rocket, while it is firing, provides a constant force, Fo, tangent to the disk, for a time t. I = 1/2mR^2.

(a) Derive an expression for change in angular momentum of the disk in terms of the given quantities and physics constants.

(b) Derive an expression for the angular speed of the disk after the rocket has fired. Give the answer in terms of given quantities and fundamentals constants.

The rocket motor has now been adjusted so that it is angled to the edge of the disk, pointed inward. Assume the rocket fires for the same amount of time and applies a force of the same magnitude.

(c) how does the final angular speed of the disk compare to the answer you found in part (b)?

Answers!!!

OK!! Here is the TEST!!

A lawnmower starter is a flywheel and a great example of our learned ability to manipulate torque!

Simply opening a door can tell us so much! We have the door handle as far away from the hinges as possible and we want to push perpendicular to the plane of the door. This is a great model as to how giving an extended object angular acceleration is not only dependent on how hard you push but also where and in what direction you push. The physical quantity that relates all of these aspects of an applied force is called the torque associated with said force. In perfect harmony with Newton’s 2nd Law, the net external torque determines the angular acceleration just as net force determines linear acceleration!!

So, we use r to denote the vector from the rotation axis to the point where the force is applied and we use the symbol (phi or theta) for the angle between the directions of r and F. It is the perpendicular component of the this force that makes the object rotate, F sin (theta). This is torque!!

Torque (tau) = rF sin (theta)

…where r is the distance from the rotation axis to where the force is applied and theta is the angle between the vector r (from the axis to where the force is applied) and the force vector F.

Torque has direction in terms of clockwise (-) and counterclockwise (+). In the photo above, part (c) shows the “line of action” of the force as the extension of the force vector through the point where the force is applied. The lever arm or moment arm is the perpendicular distance from the rotation axis to the line of action of the force, r (perpendicular) = r sin (theta) and we are left with same quantity as before.

tau = r (perpendicular) F

r (perpendicular) represents the lever arm! So the longer the lever arm, the greater the torque for a given amount of force! So even a small force can generate a large torque of the lever arm is long enough!

Now that we have a general knowledge of torque, let’s have a go at a few problems!!

(1) Marcy can deliver about 10 Nm of torque when attempting to open a twist off cap on an Orange Crush soda bottle. What is the maximum force Marcy can exert with her fingers if the bottle cap’s diameter in 2 cm?

(2) Bettina Henderson applies a horizontal force of 20 N (to the right) to the top of a steering wheel on the way to soccer practice. The wheel had a radius of 18 cm and a Rotational Inertia of .097 kgm^2. Calculate the angular acceleration about the central axis due to the force.

(3) Many 6.35 cm-diameter computer hard disks spin a t a constant 7200 rpm operating speed. The disk’s have a mass of about 7.50 g and are essentially uniform throughout with a small hole in the center. I = 1/2mr^2.

(a) if the disk reaches its operating speed 2.50 s after the drive is turned on, what average torque does the drive supply to the disk during the acceleration?

(b) calculate the change in Kinetic Energy of the disk and the average power delivered to the drive as it accelerated to operating speed.

Answers!!

(4) A block of mass m1 = 2.00 kg rests on a table that exerts a negligible friction force on the block. The block is connected with a light string over a pulley to a hanging mass m2 = 4.00 kg. The pulley is a uniform disk with a radius of 4.00 cm and a mass of .500 kg. The rotational inertia of a uniform disk is 1/2mr^2.

(a) Calculate the acceleration of each block and the tension in each segment of the string.

(b) Calculate how long it takes the blocks to move a distance of 2.25 m.

(c) Calculate the angular speed of the pulley at the instant the blocks are moved.

Answer!!

Here are a couple for home!!

(1) Shawna, a 45 kg high diver, launches herself from a springboard that is 3.0 m above the water’s surface, so that she ends up with a 5.0 m fall from rest before she reaches the surface of the water. Calculate the time it takes Shawna to descend the 5 m to the surface of the water and the angular speed that will allow Shawna to complete 2.5 turns while in the air!

(2) Sarah’s potter wheel is mounted on a shaft with bearings that exert a negligible friction force, the wheel is initially at rest. A constant external torque of 75 Nm is applied to a wheel for 15 s, giving the wheel an angular speed of 500 rpm in the counterclockwise direction when viewed from above.

(a) Calculate the magnitude of the angular acceleration of the wheel in rad/s^2. What is its direction?

(b) Express the rotational inertia of the wheel in terms of the torque exerted on the wheel and the angular acceleration of the wheel.

(c) calculate the value of the rotational inertia of the wheel.

(d) The external torque is removed and a brake applied. If it takes the wheel 200 s to come to rest after the brake is applied, what is the magnitude and direction of the torque exerted on the brake?

Answers!!

OK! So, here is the answers for the cart/wheel worksheet from last week and here is a new wheels worksheet along with the answers!!!

Here is another problem with its solution, of a tension force rotating a cylinder. I also wanted to add the solution to the torque ruler scenario we went over before we left school.

I know this is a lot but it is basically all of torque. We will be here for a little bit.

Thanks so much everybody!! You all are incredible!!!

I know you’ve all been on the edge of your seats, couches and bikes in the past week wondering if both mechanical energy and momentum are conserved in a collision.

Well, the answer is…sometimes. Let’s delve.

A collision in which the internal forces are conservative is an elastic collision. In such a case both total momentum and total energy are constant. So, during a collision of this ilk, all the initial KE not required to conserve momentum is converted to U (potential energy) and, after the collision, all the U is converted back to KE. Think about our mini-billiard balls colliding!

Now, let’s think about a “fruit fight”. If two apples are traveling horizontally through the air and they collide, they will explode. Our flying fruit have no chance to return to their original form, in some cases they might even stick together. This is an example of an inelastic collision and it is here where mechanical energy is not conserved and we say KE has been dissipated. And we can quantify the amount of KE that was lost by comparing the KE before the interaction with the KE after the collision. If the objects stick together, it is referred to as a completely inelastic collision and we use the combined mass in the kinetic energy equation.

So let’s take a look at the interaction between Sydney and Jaromir again here, along with another example of a head-on collision during a stunt scene in Mission: Impossible 13; Zero Velocity, to see if we can grasp the concept.

In filming Mission Impossible 13: Zero Velocity, a 1500 kg car moving north at 35.0 m/s collides head on with a 7500 kg truck moving south at 25.0 m/s. The car and the truck stick together.

(a) How fast and in what direction is the wreckage traveling just after the collision?

(b) How much mechanical energy is dissipated in the collision?

Have a go…A large bass with a mass of 25.0 kg swims at 1.00 m/s towards and swallows a small fish that was stationary. If the smaller fish has a mass of 1.00 kg, what is the speed of the bass immediately after it dines? What type of collision is this? What is the percentage of kinetic energy dissipated, if any? Answer

And finally, I wanted to end with a look at how collisions in two dimensions can be quite daunting. I would love for you to appreciate this complexity qualitatively more than quantitatively for the moment!!

Thanks for being such amazing students!!

This video depicts was one of my best Halloween costumes. I even had the squash racquet!! I lost the contest to a Banana but I love airport walkways! The feeling of being fast or the accomplishment of treading against the moving earth are exhilarating!!

If you recall, in linear motion with constant acceleration, we were able to use a set of equations that related position, velocity and acceleration for analysis. Similarly, in rotational motion with constant angular acceleration, the same relationship appears for the rotational equivalents of the corresponding quantities in straight-line motion!! Therefore, we can define angular acceleration as the rate at which the angular velocity changes with respect to time in much the same way that we defined acceleration of an object moving in a straight line.

Now just as in straight line motion, a positive value of angular acceleration does not necessarily mean the extended object’s rotation is speeding up and a negative value doesn’t necessarily correspond to slowing down. If angular velocity (w) and angular acceleration (alpha) have the same algebraic sign, the extended object is speeding up. Conversely, if w and alpha the opposite sign, the object is slowing down. Now, let’s have go at the spinning top example!!

OK!! Let’s think practically and qualitatively about what’s happening here (also a bit old school!).

Optical disk drives, such as CDs and DVDs, have information stored in small depressions “burned” onto the disk surface. Hence the term, “burning a CD” which is what we were doing when we downloaded songs off Napster at the turn of the century! Anyway, a laser is used to detect changes in the depth on the surface as the disk spins. A change is interpreted as a 0 and no change in depth is interpreted as a 1. There are millions of these burns on a disk’s surface and the DVD player retrieves this stored information. Now, these optical technologies are designed to maintain a constant rate of information retrieval. If the laser samples depth on the surface at constant intervals of time, why do you think the angular velocity of the disk cannot be constant?

Let’s see if we can answer these questions!!

(1) Orla pushes a merry-go-round that has a diameter of 4.00 m and goes rest to an angular speed of 18.0 rpm in a time of 43 s.

(a) Calculate the angular acceleration of the merry-go-round in rad/s^2.

(b) Calculate the angular displacement (in radians) of the merry-go-round during this time interval.

(c) What is the maximum linear speed of Orla if she rides on the edge of the platform?

(2) Interpreting Data!!

I have provided the answers for the Pure Roll worksheet and the notes for the Hoop and Disk race scenario about rotational inertia. I have also written out a couple of problems that might put a bow on these moments (of inertia).

Thanks so much!! Y’all are wonderful!!

Please enjoy this feature of Mr. Burns driving and colliding with everything!!

“Once a song gets momentum and gets away from you, that’s a good sign” – Dave Matthews.

“What?” – Darren

So let’s begin our discussion about momentum by defining a collision as any interaction where the internal forces dominate. If a hockey player checks another, the internal forces are strong enough to seriously injure the other player. The external forces of friction very minimal. Also evident in the tennis serve, the ball and the racquet forces are so large that the ball distorts noticeably. However, by comparison, the external forces of gravity on the ball and your hand on the racquet are very insignificant.

In summary, if the internal forces during a collision are much greater in magnitude than the external forces, the total momentum of the interacting objects has the same value just before as just after the collision. This means that momentum is conserved and leads us to one of the incredible fundamental laws that governs the interactions of all objects in the universe, the Law of Conservation of Momentum.

So, I wanted to give you a couple of problems to work on. This unit is all about practice and keeping track of your direction and your variables. Good luck!!

(1) Blythe and Bart are ice skating together. Blythe has a mass of 50 kg and Bart has a mass of 80 kg. Blythe pushes Bart in the chest when both are at rest, causing him to move away at a speed of 4 m/s. Determine Blythe’s speed after she pushes Bart?

(2) A 2 kg object is moving east at 4 m/s when it collided with a 6 kg object that is initially at rest. After the collision, the larger object moves east at 2.00 m/s. What is the final magnitude and direction of the velocity of the smaller object after the collision?

Thanks so much everyone!! You’re doing amazing!!